Wavicles
One of the most important conceptions of matter and energy to come out of this century, besides the fact that they are interchangeable states of the same thing (expressed in Einstein's famous equation, E=mc2) is the fact that either state can act as either a particle or a wave. This was a very perplexing problem, and still remains so if we try to visualize what matterenergy looks like at the elementary level. A particle is localized in spacetime -- it can be assigned very distinct coordinates, and even thought of as stationary and static. A wave is not localized and cannot be static.
The wave-particle duality is an example of the complementarity principle in quantum theory. An electron, for example, will either act like a particle or a wave, but never both at the same time. If we use a particle detector to see the electron, it will be a particle, and if we use a wave detector, it will be a wave. Somehow, we must think of the electron as being both, but in its ability to display both modes of mutually exclusive states of being, it is actually neither. The essence of what the electron really is must be something else entirely. Whatever that is, is quite impossible to visualize, and has been dubbed a wavicle.
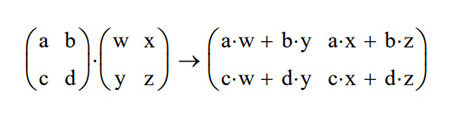
The way this duality is dealt with in physical theory is to use a mathematical entity called a quon which has the characteristic of both a particle and a wave. Conceptually, it is a bundle of three vectors, three polarities, represented by a matrix. This requires quantum theory to use the mathematics of matrix mechanics.



